Two young people leave their homes to become students at a distant school. Each has received the same advice that Polonius gave his son Laertes: "Neither a borrower nor a lender be, For loan oft loses both itself and friend, And borrowing dulleth th'edge of husbandry." (Husbandry is careful or thrifty management.) Good advice, but away from parental guidance, one becomes a borrower and the other a lender.

Mike throws a party for all his new friends, and charges the food and drink on his credit card. Added to his travel and car expenses, the bill is staggering, so he pays the minimum, and "carries a balance" of $1 000. In effect, Mike has borrowed $1 000 from the bank that issued the card.

Jennifer receives a scholarship check from an organization in her home town, and deposits $1 000 in a savings account at the same bank, making her, in effect, a lender. The consequences can be expressed in terms of compound interest paid by Mike, and received by Jennifer.

In the compound interest equation, P is the principal, the amount on which the calculation of interest is based; S is the sum that results from the calculation; i is the interest rate; n is the number of days, quarters, or years.

S = P ( 1 + i ) ⁿ

The credit card bill that Mike receives after 30 days shows S, the amount he owes. The interest charged on this particular card has an annual rate (APR) of 10.240%. Percent means “per hundred”, so 10% = 0.10 in ordinary numbers. The daily rate is:

i = ^0.1024/_{365 days/year} = 0.00028050547 / day

Use the y ^x key (or x ^y ) to calculate an exponential quantity.

S = $1 000 (1.00028050547) ³⁰ = $1 000 (1.008450766) = $1 008.45

Mike now owes $1 000 plus $8.45 interest.

Jennifer finds interest credited to her account after 30 days. It was calculated with APR = 1.25%;

i = ^0.0125/₃₆₅ = ^0.000034246/_day

(Step missing here. Can you supply it?)

S = $1 000 X 1.0010279 = $1 001.0279

Her account has grown by $1.03. Compare with the interest paid by Mike. Have you ever wondered why there are so many banks?

Rates of gain or loss in the value of property can be found with a modification of the compound-interest equation, by taking the logarithm of both sides, and rearranging:

S = P ( 1 + i ) ⁿ

log S = log P + n log (1 + i )

The logarithm of a number is the power of 10 equivalent to that number:

1 000 = 10 ³;  log 1 000 = 3.                

Repeat after me: A logarithm is an exponent . A logarithm is an exponent.

In the original equation, n is an exponent. Taking logs brings it down to earth, into an ordinary number position .

Next, rearrange:

log (1+i) = (log S - log P) / n

After finding the value of log (1+i),  use the antilog or 10 ^x function on the calculator to find 1+i. Then merely subtract 1 to get i, the rate of appreciation or depreciation.

For example, a homeowner sells his property for $500 000; he bought it 16 years before for $110 000.

log (1+i) = (log 500 000 - log 110 000)/ 16 y = (5.698970004 - 5.041392685)/16 =  0.041098582

1+i = antilog 0.041098582 = 1.099255336

(Subtract 1.)

 i = 0.0992/year = 9.92%/yr

Of course, this apparent rate of appreciation is partly due to inflation, which has varied from 1.3 to 2.9 percent per year in recent years.

Mike's car was bought 8 years ago for $9 950, and now has a book value of $2 210. He has appreciated having a car, but the car has not appreciated. The depreciation rate is:

log 1+i = ^-0.653430807/_8y = -0.08167885

1+i = 0.828554631,  i = -0.171445368/yr

His car has depreciated at a rate of 17.1 % per year, an asset to his social life, but a poor investment.

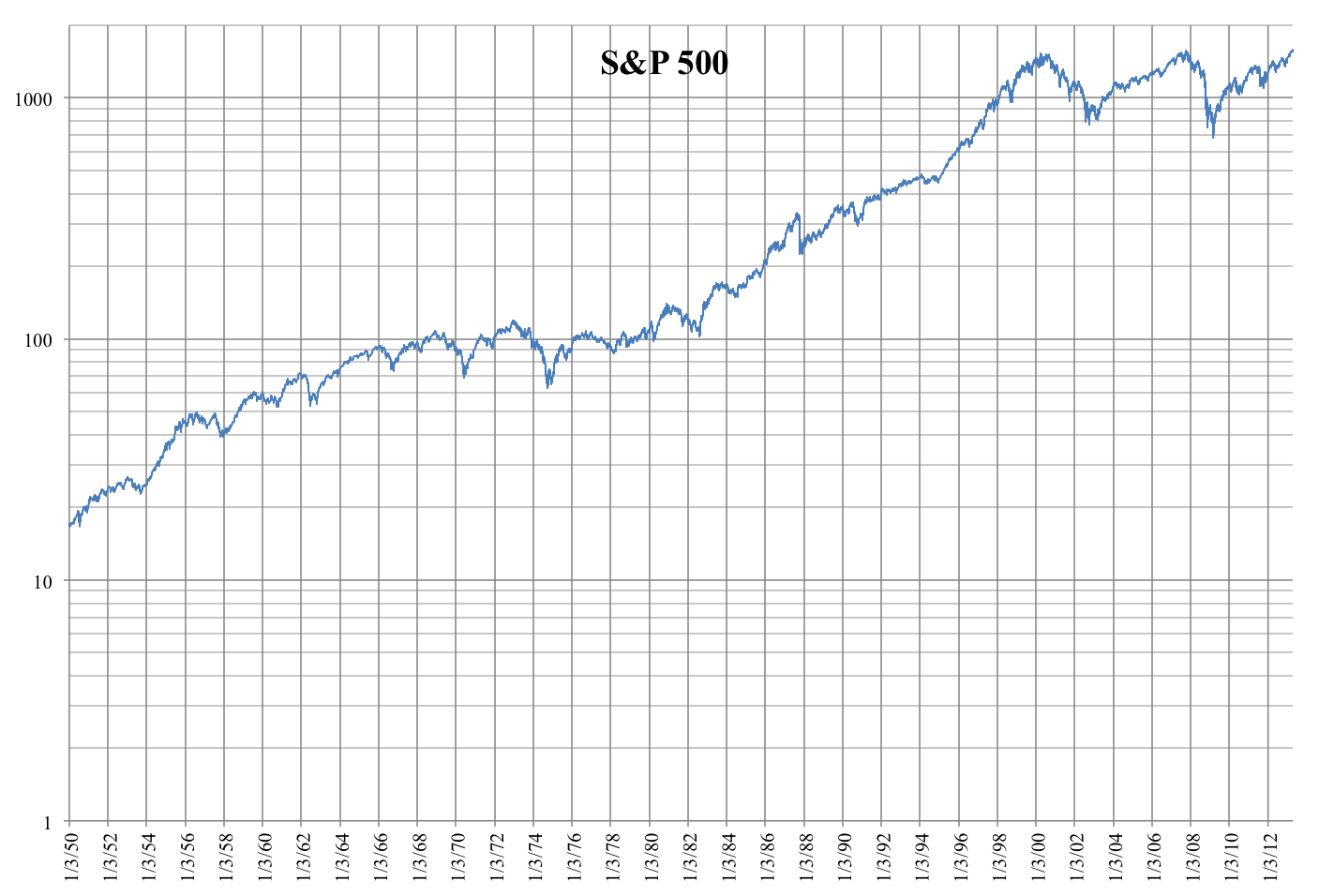
Shares of stock in corporations tend to increase in value in the long run (Fig. 6-1). Average selling prices, representative of the stock market in general, are reported as S&P 500, Dow-Jones, etc. Over some periods, your investment grows rapidly, especially if you re-invest dividends instead of spending them. The compound interest equation allows calculation of the rate of appreciation. The graph shows that $1 invested in 1926 grew to $2 053 in 2001:

log(1+i) = (log 2 053 - log 1) / 75 = 0.044165185

1+i = antilog 0.044165185 = 1.107044774

i = 0.1070 = 10.7 % per year

Not bad, but who wants to wait 75 years, in this age of instant gratification?

The logarithm of a number is the power of 10 equivalent to that number. Here is a nice theorem that illustrates the meaning of logarithm and the meaning of proof:

THE LOGARITHM OF 2 IS IRRATIONAL.

By irrational we mean that it cannot be expressed as a ratio of whole numbers, such as ¼, ½, ¾ etc. By logarithm we mean that this ratio, if it exists, serves as the exponent of 10.

 Assume that such a ratio of two numbers p and q exists:

log 2 = p/q

10 ^p/q = 2

Raise both sides to the q power: (pq /q = p)

10 ^p = 2 ^q

This is impossible, because all powers of 10 end in 0, and all powers of 2 end in 2, 4, 6, or 8. Therefore, the assumption is wrong. Such a ratio cannot exist. QED.

Quod erat demonstrandum = “Which was to be demonstrated”, a Latin phrase signifying that the proof is complete.

There are ratios, such as 31/103 and 497/1651, almost the same as log 2, but "not exactly".

QED also stands for quantum electron dynamics. Avoid this usage, unless you love physics.