Chapters
- 1. Height and weight
- 2. Uses of the SI
- 3. Numbers and letters
- 4. Plain geometry
- 5. Circles
- 6. Compound interest
- 7. Population growth
- 8. Solid geometry
- 9. Molecules
- 10. Radioactive decay
- 11. Pressures
- 12. Gene frequency
- 13. Energy
- 14. Summary
Sections
Pythagorean Theorem
In a world of opinion, conjecture, guesswork, and lies, the only certainties are death and taxes. No, there is one other certain thing: the Pythagorean theorem. It specifies the lengths of the sides of a right triangle. The square on the hypotenuse is exactly equal to the sum of the squares on the other two sides. The hypotenuse, from υποτεινω, meaning to prop up, is the slanted side opposite the right angle. The perfect right angle is found only in geometry, but anything standing upright, like the wall of a building, or a tree trunk, or a soldier at attention, forms an approximate right angle with the base. In any spatial arrangement that looks like a right triangle, the theorem gives us the ability to calculate a length or distance that may be difficult or impossible to measure.
Suppose that a triangular area has sides that are 5 and 12 meters long; what is the length of the third side, the hypotenuse? In the notation of algebra:
x2 + y2= z2
52+ 122= 25 + 144 = 169 = z2
Realize that z, the length of the hypotenuse, is not 169; z is the square root of 169, symbolized
Use of the square root command on the calculator gives = 13.
Thus, the length is z = 13 m. The x2 button verifies this: 132 = 169.
The square root sign is your friend. It asks: What number, when multiplied by itself, will produce the designated number?
Sometimes the hypotenuse is known, and its length is used to calculate the length of one of the other sides. If the triangular area has a side of 15 m and hypotenuse of 17 m:
152 + y2 = 172
y2= 289 - 225 = 64
y = = 8 m
Exercise 4-1. Find the missing Pythagorean numbers:
| x | y | z |
|---|---|---|
| 3 | 4 | _ |
| 8 | _ | 17 |
| _ | 21 | 29 |
| 9 | 40 | _ |
An antenna 10.1 meters tall needs a guy wire to brace it. If the wire is anchored 5.50 m from the base, and extends to the top, what length of wire is needed? Call the height of the antenna a, and the distance on the ground b; then the wire is the hypotenuse c, and the Pythagorean relation is:
c2= a2 + b2.
c 2 = 10.12 + 5.502= 132.26 m2
c = = 11.50 m, the length of the guy wire.
Calculating Area
When a home space needs to be painted, papered, carpeted, or tiled, the problem is to calculate area. If the space resembles a square with a side of length ( L) = 2.45 m, the answer is : L2 = 2.452= 6.00 m2. If the space is rectangular, the length and width are multiplied together:
L X W = 2.45m X 3.35m = 8.21 m2.
The floor area of a house or an apartment is often an important factor in determining its value, and the correct amount of homeowners insurance . If the rooms are not rectangular, the calculation of total area can be tricky. A good strategy is to make a sketch showing dimensions, then divide the spaces into rectangles and triangles . The areas of each of the parts can be calculated separately, then added. The area of a triangle (A ) = bh/2 (1/2 the product of base and height).
Exercise 4-2. With the dimensions given on Fig. 4-1, calculate the floor area of the little sunroom, and the whole space shown.
Examples
The Leaning Tower of Pisa (Fig. 4-2) was built to a height of 54.50 m. Because of the tilt, an object dropped from the top now lands 5.034 m from the base. Take the original height as the hypotenuse, and the present vertical height as side a. How far does the object fall ?
a2 = c2 - b2= 54.502 - 5.0342 = 2 944.908844
a = = 54.267m
Galileo dropped two balls, one wood and one iron, from the top, and found that they hit the ground at the same time (Fig. 4-2). Given the value of a above, how long did it take for the balls to drop? The modern value for the acceleration of gravity is 9.80 m/s2. (54.267m/ 9.80 m/s2 = 5.53775 s2 ) Calculation gives 2.35 seconds.
Any elevation above sea level makes it possible to see farther out to sea.. The seaman in the crow's-nest observes a more distant horizon. In Figure 4-3, r = the radius of the earth, x = the elevation of the observer, and y = distance to the horizon.
A person standing on the beach has eye level x = 1.524 m. An average radius of the earth is 6 371.406 km . From the Pythagorean theorem :
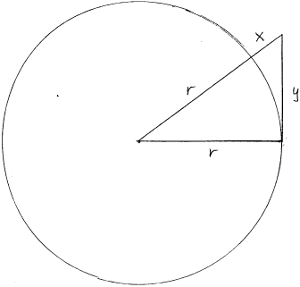
r2 + y2 = ( r+x ) 2.
Note that x must be expressed in km before adding it to r, and that the addition must be done before r+x is squared.
y2 = (6 371.407524)2 - (6 371.406)2 = 19.4189
y = = 4.4067 km (2.738 miles)
This is the distance to the horizon for a person standing on the beach. Marilyn Vos Savant answered this question in her column of June 15, 2003, and she was right, as usual.
Mike and Jennifer are stuck on top of the Wonder Wheel at Coney Island.
Mike: I think we can see about five times farther than anyone on the beach.
Jennifer: Let's work it out. I always keep my calculator in my backpack.
Exercise 4-3. Calculate distance to the horizon from the top of the Wonder Wheel, height x = 150.0 ft = 45.72 m.
Jennifer: I get 24.140 km, or 15.00 miles.
Mike: You're a nerd, and I love you.
Exercise 4-4. Mount Pinos, near Los Angeles, California is 8 831 feet in height. Convert to km, and calculate the distance to the horizon for a person on the summit.